No se deje engañar por conclusiones descabelladas

Estamos acostumbrados a leer informes de que se han realizado investigaciones y los participantes han mostrado un efecto. Los participantes del grupo experimental superaron a los participantes del grupo de control. A menudo, el informe agrega que el efecto fue estadísticamente significativo, tal vez al nivel de 0,05 o incluso al nivel de 0,01.

Por lo tanto, es fácil tener la impresión de que todos los participantes mostraron un efecto. Sin embargo, eso estaría mal.

En las pruebas de significación estadística, los valores de p (y los tamaños del efecto) son esencialmente la diferencia entre las medias de los grupos dividida por (o expresada a través de) la desviación estándar. Significación estadística en relación con los valores medios del grupo. Entonces, ¿en qué medida la diferencia entre las medias de los grupos refleja las diferencias entre los individuos?

Es posible que todos los participantes mostraran un efecto, pero solo en una medida muy pequeña, y un gran número fue suficiente para obtener significación estadística. Los estadísticos están preocupados por esta posibilidad y han inventado mediciones del tamaño del efecto para dar cuenta de este hallazgo. Desafortunadamente, pocos informes, especialmente en los medios, incluyen información sobre el tamaño del efecto, probablemente porque agregar más detalles como este solo distorsiona la imagen y confunde al lector.

Es posible que solo algunos de los participantes mostraran un efecto, pero lo mostraron en gran medida, contrarrestando a aquellos que no mostraron ningún efecto. Las mediciones simples de la variabilidad mostrarán si este puede ser el caso, pero nuevamente, muchos legos no entenderán ni se preocuparán por el significado de la variabilidad, y la mayoría de los informes que reciben no incluyen desviaciones estándar.

Entonces, probemos un enfoque diferente para que los lectores comprendan fácilmente cuán generalizado es el efecto.

Para investigar esta pregunta, obtuvimos datos de un estudio financiado (no realizado por nosotros) que comparó dos grupos en términos de desempeño en una tarea que AI (grupo experimental) o sin la ayuda de un sistema de IA. Había 30 participantes en cada grupo, un número aceptable. Se eligió este conjunto de datos en particular porque las distribuciones parecen ser aproximadamente normales (usando la prueba del globo ocular).

Puedes ver los resultados a continuación. La distribución de la condición experimental se muestra en azul y la distribución de la condición de control se muestra en naranja. La figura muestra que las dos distribuciones se superponen en gran medida.

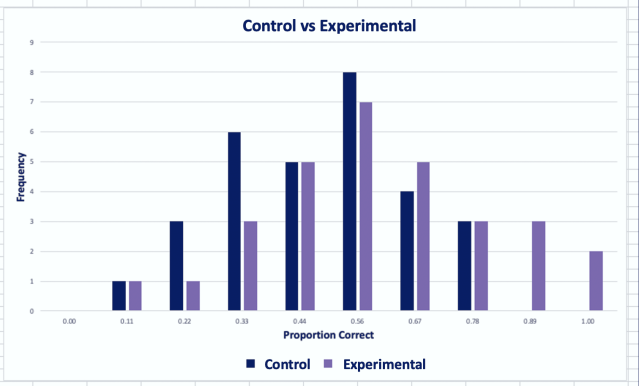
Distribuciones superpuestas para grupos experimentales y de control.

Fuente: Robert Hoffmann

Así que aquí hay un efecto, y es estadísticamente significativo: p<.001, usando una prueba t de dos colas. Pero definitivamente no es universal. Debemos tener esto en cuenta cuando discutamos tales hallazgos.

Pero, ¿qué se necesita para que desaparezca este efecto significativo en el nivel de p<0,001?

método de pelado

Podemos deshacernos gradualmente de los extremos. Primero, eliminamos los datos de los dos participantes del grupo experimental que obtuvieron la puntuación más alta y de un participante del grupo de control que obtuvo la puntuación más baja.

Bingo.

La proporción de respuestas correctas en el grupo experimental bajó del 65% al ​​54%, y la proporción de respuestas correctas en el grupo de control aumentó ligeramente, del 48% al 49%, y ahora la prueba t muestra una p<0,334. Ni siquiera cerca de ser considerado estadísticamente significativo. Entonces, el "efecto" inicial no parece muy confiable.

Si aún se consiguiera significación estadística después de este primer pelado, podríamos continuar pelando y contando hasta cruzar el nivel de p<0,05. Es posible que descubramos que tuvimos que hacer mucha exfoliación. En ese caso, tendríamos mucho más confianza en la conclusión sobre la significación estadística. Pero si la significancia estadística desaparece simplemente porque se excluyen tres de los 60 participantes, ¿qué tan en serio podemos tomar los resultados? ¿O qué tan en serio debemos tomar la prueba t?

Este método general se puede convertir en una «métrica» ​​proporcional real, es decir, el número de «pasos de limpieza» en relación con el tamaño total de la muestra. En este caso, este número es 3/60. Cuanto menor sea este número, más débil será el efecto estadístico.

Nota: No hemos seleccionado este ejemplo. Solo necesitábamos un conjunto de datos simple que produjera resultados estadísticamente significativos. No teníamos idea de antemano que el ejemplo ilustra tan bien nuestra tesis.

Conclusión

Para los lectores legos de informes de investigación psicológica, el método peelback puede ser mucho más fácil de entender que otros tipos de estadísticas, como el tamaño del efecto.

Los propios investigadores pueden encontrar un ejercicio útil para explorar y aprender el método peelback para sus propios experimentos. Si tienen suficiente coraje. Luego, los investigadores podrían determinar qué participantes eran responsables de los hallazgos y cuáles eran esos participantes.

Pero pensemos de nuevo en lo que implica el peeling. Algunos libros de texto de estadística se refieren al problema de los «valores atípicos» e incluso presentan procedimientos que permiten a los investigadores justificar la eliminación de datos de los valores atípicos. El concepto parece ser que los «valores atípicos» simplemente agregan ruido a los datos, oscureciendo los efectos «verdaderos».

Los miembros más efectivos del grupo experimental (en estudios como el que se presenta aquí) demuestran lo que es posible para los humanos. Los peores resultados tanto en el grupo experimental como en el de control pueden ser indicios de problemas motivación o elección Los «mejores» y «peores» ejecutantes son individuos que deben estudiarse más a fondo, por ejemplo, con entrevistas cognitivas post-experimentales en profundidad.

Desafortunadamente, muchos estudios psicológicos no incluyen entrevistas cognitivas postexperimentales en profundidad como parte clave de su método, e incluso cuando se realizan entrevistas, los resultados generalmente se mencionan brevemente en los informes de investigación. Los datos sobre lo que la gente piensa siempre aclaran el significado y el «significado» de los resultados numéricos.

Entonces, esta pequeña exploración de una idea simple expone algunos problemas y trampas importantes en la metodología de la investigación. Una de las más importantes es la advertencia de nunca confundir un efecto estadístico (sobre los grupos) con un efecto causal que la variable independiente pueda tener sobre los individuos.

Robert Hoffman es coautor de esta publicación.